����˼·:������(sh��)�W(xu��)�����W(xu��)֪�R������Ӌ(j��)��C(j��)���g(sh��)��Q���̼��g(sh��)���}
����Ԫ���������Ô�(sh��)�W(xu��)���Ʒ����������挍(sh��)����ϵ�y(t��ng)(�����d�ɹ��r)�M(j��n)��ģ�M�����ú��ζ�������õ�Ԫ��������Ԫ�������ޔ�(sh��)����δ֪��ȥ�ƽ��o��δ֪�����挍(sh��)ϵ�y(t��ng)��
���ކ�Ԫ��(FEM)��20���o(j��)50����ԁ��S��Ӌ(j��)��C(j��)�ďV����(y��ng)�ö��l(f��)չ������һ�N�F(xi��n)����(sh��)ֵ�ⷨ��ԓ�������ȑ�(y��ng)�����B�m(x��)���W(xu��)�I(l��ng)��һ-�w�C(j��)�Y(ji��)��(g��u)�o�� ��(d��ng)�B(t��i)���Է��������S��ܿ�͏V����(y��ng)����������(d��o)��늴ň������w���W(xu��)���B�m(x��)�Ԇ��}��
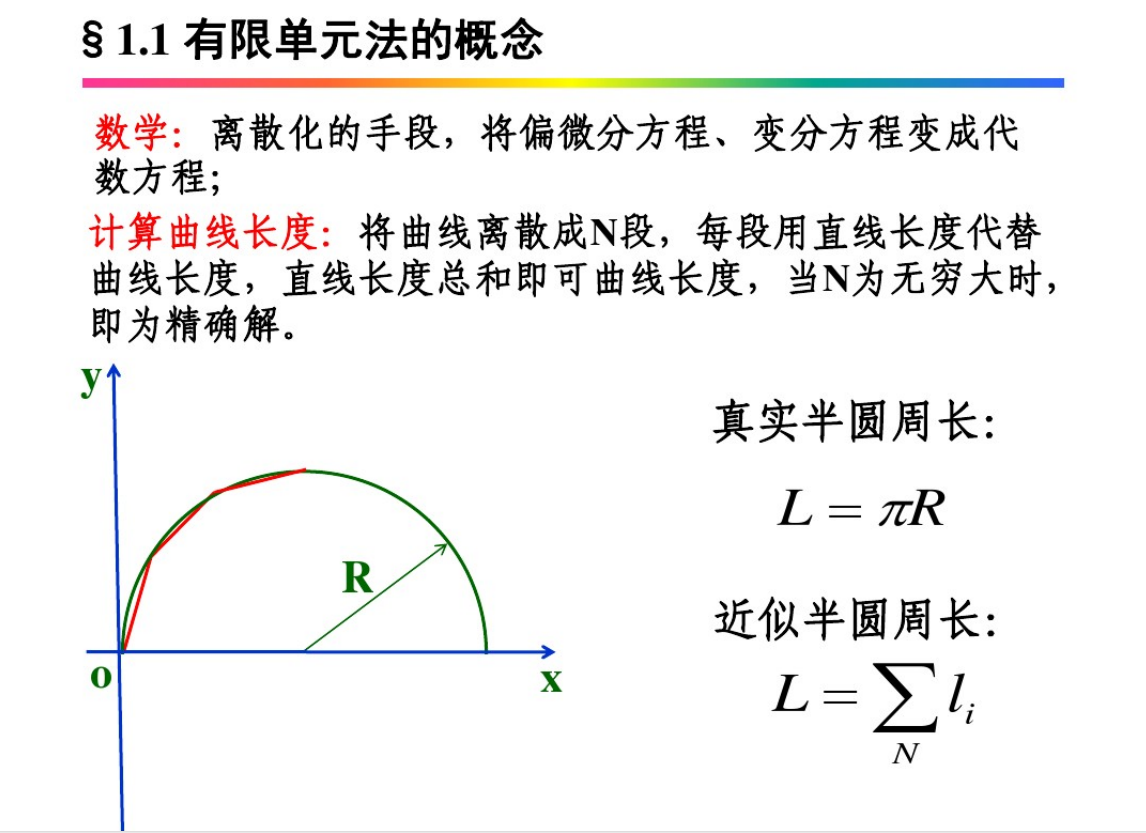
��(sh��)�W(xu��):�xɢ�����ֶ�����ƫ�ַ�����׃�ַ���׃�ɴ���(sh��)����;
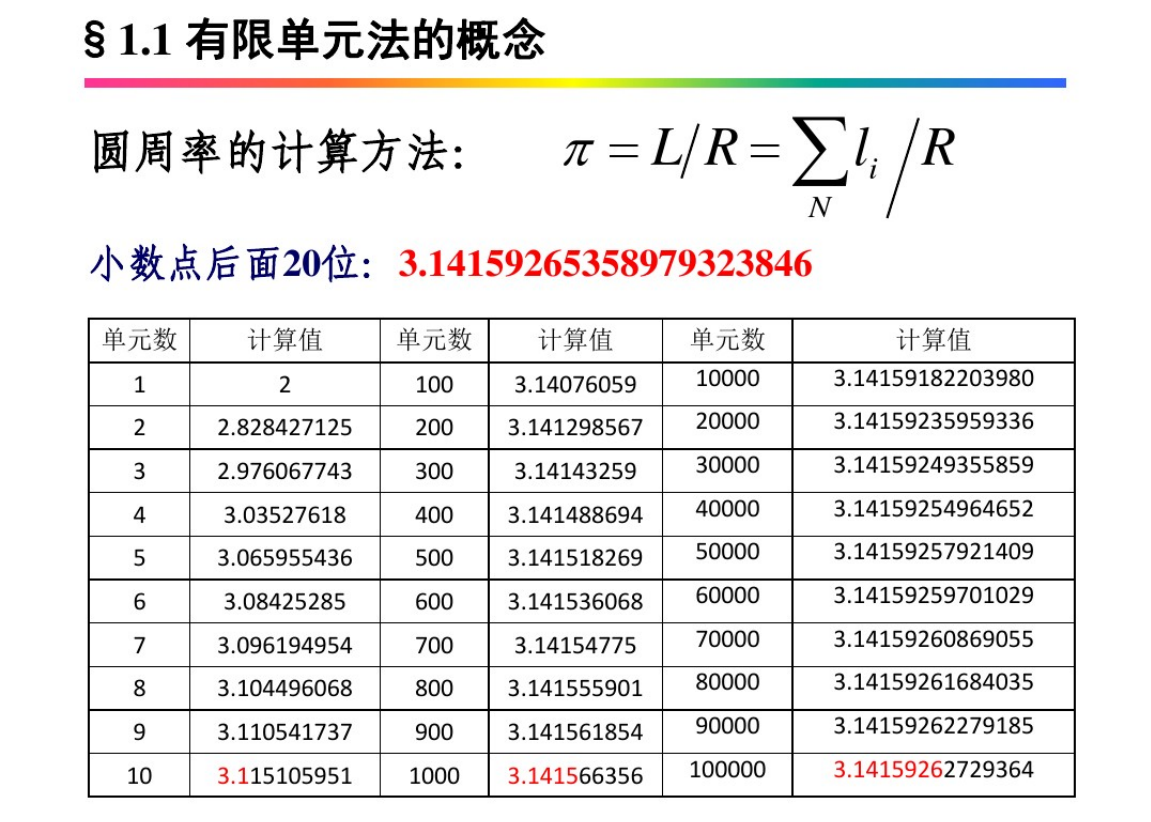
Ӌ(j��)�������L��:�������xɢ��N����ÿ����ֱ���L�ȴ��������L�ȣ�ֱ���L�ȿ��ͼ��������L������(d��ng)N��o�F��r(sh��)�����龫�_����
���W(xu��):�xɢ�����ֶ������Æ�Ԫ���W(xu��)���������B�m(x��)�w�xɢ�����ނ�(g��)��Ԫ�ĽM�ϽY(ji��)��(g��u);
�X݆�đ�(y��ng)���ֲ�:���X݆�ָ�ɺܶ���Ԫ���ɽY(ji��)�c(di��n)���B.�����f�����Ϣ�������ނ�(g��)�B�m(x��)�w�ĽM�ϴ���ԭ�����X݆�Y(ji��)��(g��u)��