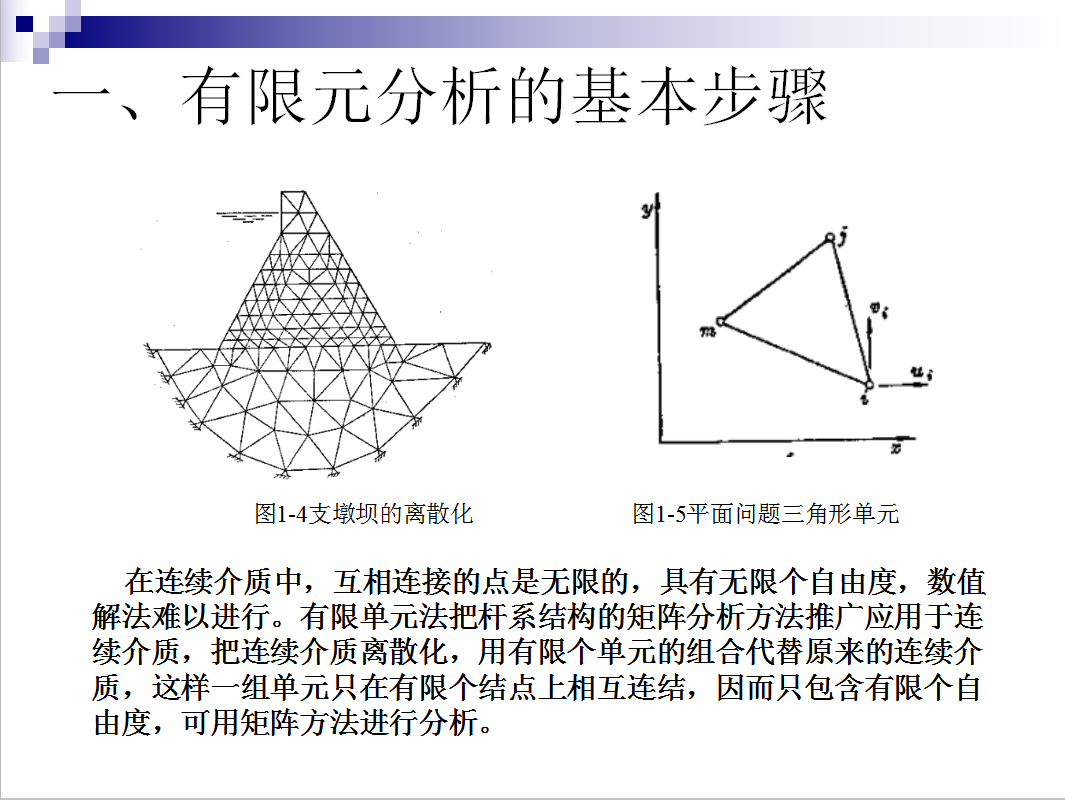
���B�m(x��)���|(zh��)�У������B�ӵ��c(di��n)�ǟo(w��)�������Пo(w��)�ނ�(g��)���ɶ�����(sh��)ֵ�ⷨ�y���M(j��n)�������ކ�Ԫ���їUϵ�Y(ji��)��(g��u)�ľ�ꇷ��������ƏV��(y��ng)�����B�m(x��)���|(zh��)�����B�m(x��)���|(zh��)�xɢ���������ނ�(g��)��Ԫ�ĽM�ϴ���ԭ��(l��i)���B�m(x��)���|(zh��)���@��һ�M��Ԫֻ�����ނ�(g��)�Y(ji��)�c(di��n)����B�Y(ji��)�����ֻ�������ނ�(g��)���ɶ������þ�ꇷ����M(j��n)�з�����
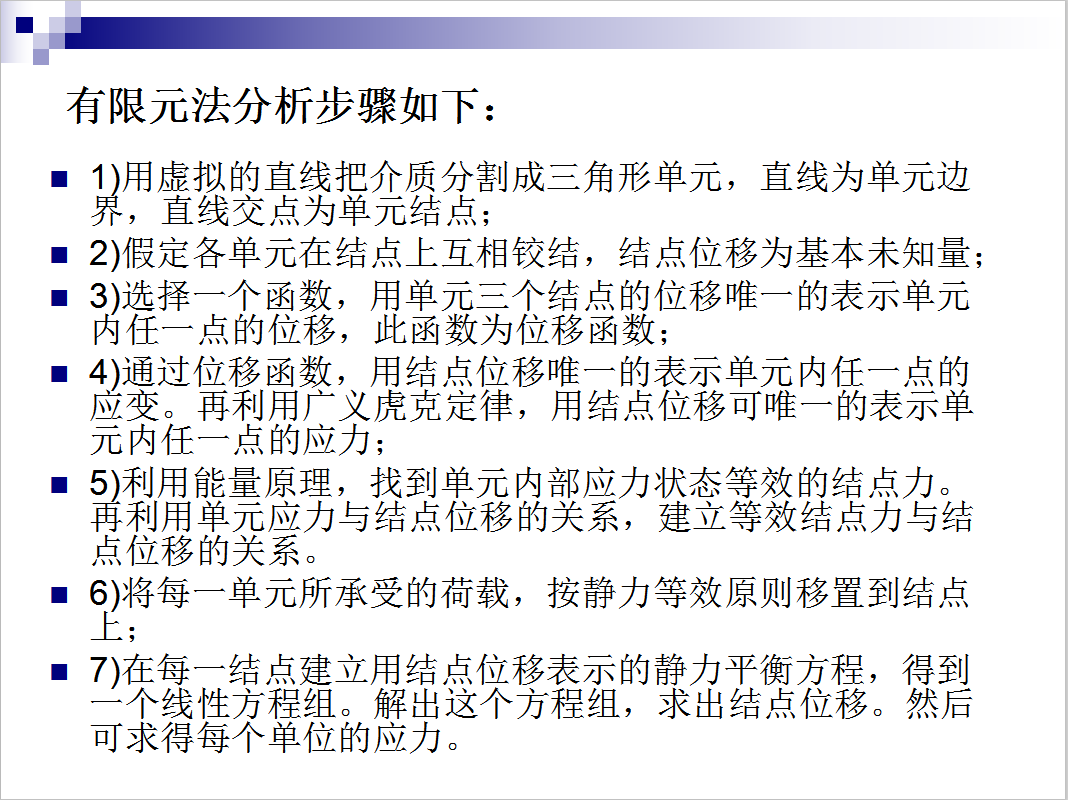
����Ԫ���������E���£�
1)��̓�M��ֱ���ѽ��|(zh��)�ָ�������Ά�Ԫ��ֱ�����Ԫ߅����ֱ�����c(di��n)���Ԫ�Y(ji��)�c(di��n)��
2)�ٶ�����Ԫ�ڽY(ji��)�c(di��n)�ϻ����q�Y(ji��)���Y(ji��)�c(di��n)λ�ƞ����δ֪����
3)�x��һ��(g��)����(sh��)���Æ�Ԫ����(g��)�Y(ji��)�c(di��n)��λ��Ψһ�ı�ʾ��Ԫ��(n��i)��һ�c(di��n)��λ�����˺���(sh��)��λ�ƺ���(sh��)��
4)ͨ�^(gu��)λ�ƺ���(sh��)���ýY(ji��)�c(di��n)λ��Ψһ�ı�ʾ��Ԫ��(n��i)��һ�c(di��n)�đ�(y��ng)׃�������ÏV�x���˶��ɣ��ýY(ji��)�c(di��n)λ�ƿ�Ψһ�ı�ʾ��Ԫ��(n��i)��һ�c(di��n)�đ�(y��ng)����
5)��������ԭ�����ҵ���Ԫ��(n��i)����(y��ng)����B(t��i)��Ч�ĽY(ji��)�c(di��n)���������Æ�Ԫ��(y��ng)���c�Y(ji��)�c(di��n)λ�Ƶ��P(gu��n)ϵ��������Ч�Y(ji��)�c(di��n)���c�Y(ji��)�c(di��n)λ�Ƶ��P(gu��n)ϵ��
6)��ÿһ��Ԫ�����ܵĺ��d�����o����Чԭ�t���õ��Y(ji��)�c(di��n)����
7)��ÿһ�Y(ji��)�c(di��n)�����ýY(ji��)�c(di��n)λ�Ʊ�ʾ���o��ƽ�ⷽ�̣��õ�һ��(g��)���Է��̽M������@��(g��)���̽M������Y(ji��)�c(di��n)λ����Ȼ������ÿ��(g��)��λ�đ�(y��ng)����